It is an empirical formula used for the calculation of ultimate load both for short and long columns. Rankin’s formula is also known as Rankin Gordon Formula. It gives the ultimate load that column can bear before failure. If column is short, calculated load will be known as crushing load. And load will be buckling or crippling load, in case of long column.
This formula only gives the ultimate load, but columns are design on safe load. In order to get safe load, divide ultimate load ( Load obtained from Rankin’s Formula) with factor of safety (F.O.S).
Rankin’s Formula
Mathematically, Rankin’s formula can be expressed as;
\(P\space\ =\space\ \frac{f_{c}A}{1\space\ +\space\ a(\frac{l}{k})^{2}}\)Where,
P = Critical Load
fc = Critical Stress
A = Cross-sectional Area of Column
\(l\space\ = Equivalent\space\ or\space\ Effective\space\ Length\space\ of\space\ The \space\ Column\)K = Least Radius of Gyration
a = Rankin’s Constant: It depends on the material of column.
For different materials, vale of “a” are as following;
For Mild Steel = a = 1/7500
For Cast Iron = a = 1/1600
For Wrought Iron = a = 1/9000
Rankin’s Formula Example
A column of a building looks not safe. CEO of a company hired civil engineer to check whether the column is safe or not. Column is of mild steel whose length is 3 meters and both ends are fixed. Load coming on that column is 400 N. Critical stress coming on that column is 320×10^2 Newton/meter square. Cross-section of column can be shown below. Now, check whether column is safe or not?
Given Data
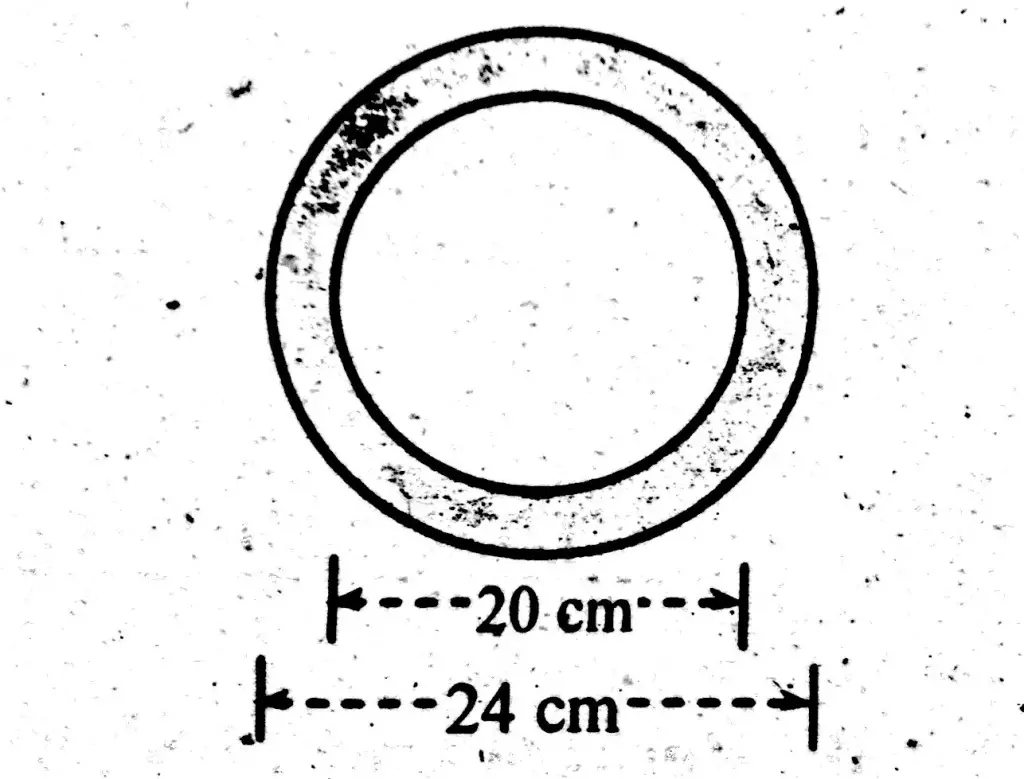
External diameter of a column = D = 24 cm
Internal diameter of a column = d = 20 cm
Length of column = L = 3m = 300 cm
Critical Stress = fc = 320 x 10^6 Newton / sq.meter = 32 KN/sq.meter
As column is of mild steel. Value of Rankin’s Constant;
a = 1/7500
Required
Critical Load = P = ?
Solution
First, calculate the equivalent length(effective length);
- Equivalent Lenght
Equivalent Lenght = 150 cm
- Cross-section Area
Put value of external and internal diameter.
\(A\space\ =\space\ \frac{\pi}{4}(24^{2}\space\ -\space\ 20^{2})\)A = 138.23 centimeter square
- Radius of Gyration
Radius of Gyration can be calculated by using formula;
\(K\space\ = \sqrt{\frac{I}{A}}\)Now, calculate the least moment of inertia. In the design of columns, least radius of gyration is used. For that, take least value of moment of inertia.
\(\small Least\space\ moment\space\ of\space\ Inertia\space\ =I=\space\ \frac{\pi}{64}(D^{4}-\space\ d^{4})\)Put the required values;
\(\small Least\space\ moment\space\ of\space\ Inertia\space\ =I=\space\ \frac{\pi}{64}(24^{4}-\space\ 20^{4})\)\(I = 8432.035\space\ cm^{4}\)
Now put values of I & A in least radius of gyration formula;
\(k\space\ =\sqrt{\frac{8432.035}{138.23}}\)K = 7.81 cm
- Crushing Load
Use Rankin’s Formula for the calculation of critical load;
\(P\space\ =\space\ \frac{f_{c}A}{1\space\ +\space\ a(\frac{l}{k})^{2}}\)By placing values;
\(P\space\ =\space\ \frac{32\times\ 138.23}{1\space\ +\space\ (\frac{1}{7500})(\frac{150}{7.81})^{2}}\)
Crushing Load = P = 4216 N
Load obtained is crushing load, because length of column is less than 15 times the diameter of column