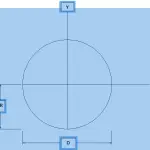
Moment of inertia of a circular section can be calculated by using either radius or diameter of a circular section around centroidal x-axis or y-axis.

Example

Find the moment of inertia of a circular section whose radius is 8” and diameter of 16”.

Solution

Moment of inertia of a circular section is same around both centriodal axis. This is because of symmetry of a section around both axis.

Therefore, moment of inertia about centroidal x-axis.

\( I_{x_{0}}= \frac{\Pi R^{4}}{4}= \frac{\Pi D^{4}}{64} \)

….

\( I_{x_{0}}= \frac{\Pi R^{4}}{4}= \frac{\Pi \times 8^{4}}{4} \)

….

\( I_{x_{0}}= 6.28\space in^{4} \)

…..

\( I_{y_{0}}=  I_{x_{0}}= 6.28\space in^{4} \)