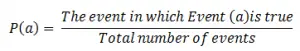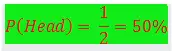What is it, everyone has a sense. There are several formal definitions of probability. Let a weather forecast man says that next day there is a 50% chance of rain. Now what this 50% actually is? It’s a probability that may be rain or not. He’s actually giving us the probability.
Now how we interpret that 50%. There are couples of ways to interpret the 50% probability of rain. It could be that if 100% he’s sure about rain tomorrow then 0% is not assure that rain tomorrow. Now that 50% kind of mean that he’s neutral between those two kinds of probabilities that it may be rain or not. So, it could be one definition that how much or how strongly you believe.
Another way of interpreting this is the frequent school of thoughts. If weather man runs the same experiment 100 times and get the same results in return, then this mean 50 out of 100times is a rain next day.
Notations of probability is;
This could be true in most of the cases.
Let another notation after rolling a dice. Here the probability of an even number. P(even) = ?
Let use the above definition that says the event in which even is true.
Total number of events when rolling a dice = 1, 2, 3, 4, 5, 6
Now when even is true = 2, 4, 6
Hence, there are three events out of six in which even events are true.
Probability definition becomes;
The above definition is true in most of the problems that are equally likely. Here, equally likely means the same probability of occurrence of each event of the sample. There could be a situation where six sides of a dice are not equally weighted. In that case, you would not be able to use the above definition of probability.
Now let modify it only for equally likely events.
So, in order to hold this definition each of the six circumstances has an equal chance of occurring.
Probability Problems:
- If flipping a dice than what is the probability of head when head and tail are equally likely?
Solution:
That one is pretty easy
P(H) = ?
So, by definition we’ll find out of total number of events in which head is true.
Total events = {H, T}
P(H) = 1
Therefore, it is likely to say that if an experiment is conducted hundred times than 50% of it we’ll get a head and the reason why we get these percentages? This is because probability of event head is as equal as the probability of tail.