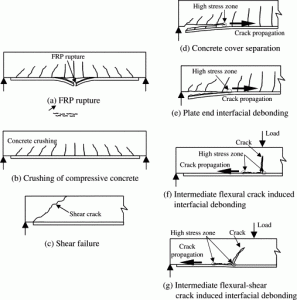
Most of the reinforced beams cracks because of a loading that are well below the service level. Restrained shrinkage becomes one of the possible reasons for cracking in members. Flexural cracking is not only because of loading but, it also depends on the reinforcement that should be used effectively.
Before knowing about flexural cracking, one should be familiar about the modular ratio. It is the ratio between the elastic modulus of steel and concrete. It is represented by ‘n’ and for most common materials its value is approximately ‘8’. Stress in steel depends on the modular ratio. It is generally ‘n’ times the stress in adjacent concrete.
Mathematically;
Cracking propagation patterns
For the concrete that is close to its point of rupture, say 520 Psi then the stress in the steel will be 8*520= 4160 Psi. In case of normal service dead and live load, the stresses in steel are expected to be 8 or sometimes even ‘9’ times the value of rupture concrete.
If the beam is well designed, then flexural cracks will be fine i.e. a hairline cracks. Hairline cracks are very small that are almost invisible to the casual watcher. As the load increases above the cracking load than it wider the crack and also increase in number of cracks. If loads are increased further, crack width increases further more. Now the number of cracks becomes less stable and it changes from a hairline crack to major cracks.
Observed Flexural cracking pattern
Cracking of concrete is not a uniform process. It proceeds randomly and highly variable and behavior may change with an abrupt changing in various factors. Therefore, cracks width can be predicted after carrying out various ACI specified tests. There are various equations too, that predict the maximum crack width.
