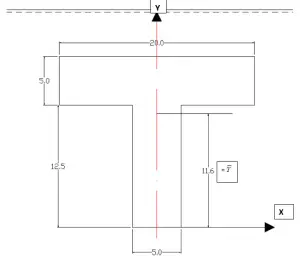
Centroid of T-section can be found easily with respect to reference x-axis. This is so because T section is symmetrical about Y-axis.
Centroid of T Section Example
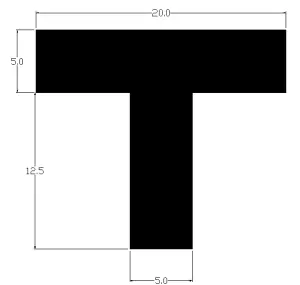
Find the centroid of T-section as shown below. All units are in cm.
Centriod of T-section
Solution
T-section is comprised of two rectangles.
Area of Large Rectangle = 20×5 = 100 cm.
Area of smaller Rectangle = 12.5×5 = 62.5 cm.
Sum of Area = 100 + 62.5 = 162.5 cm.
Centroid of Large Rectangle with respect to reference x-axis = Y = 12.5/2 = 6.25 cm.
Centroid of small rectangle with respect to reference x-axis = Y = 5/2 + 12.5 = 15 cm.
Moment of Area of Large rectangle = M1 = 62.5×6.25 = 390.25 cm.
Moment of Area of small rectangle = M2 = 100×15 = 1500 cm.
Sum of Moments = 390.25 + 1500 = 1890.625 cm.
\(\bar{Y}=\frac{Sum\space\ of\space\ of\space\ Moments}{Sum\space\ of\space\ of\space\ Area}\)\(\bar{Y}=\frac{1890.625}{162.5}=11.63cm\)
As shown below;
