Column is a long cylindrical member subjected to axial compression. Column carries self-weight and load coming on it. Generally, load transfers through its longitudinal direction. Column is categorized based on its height. These are;
- Short Column
- Long Column
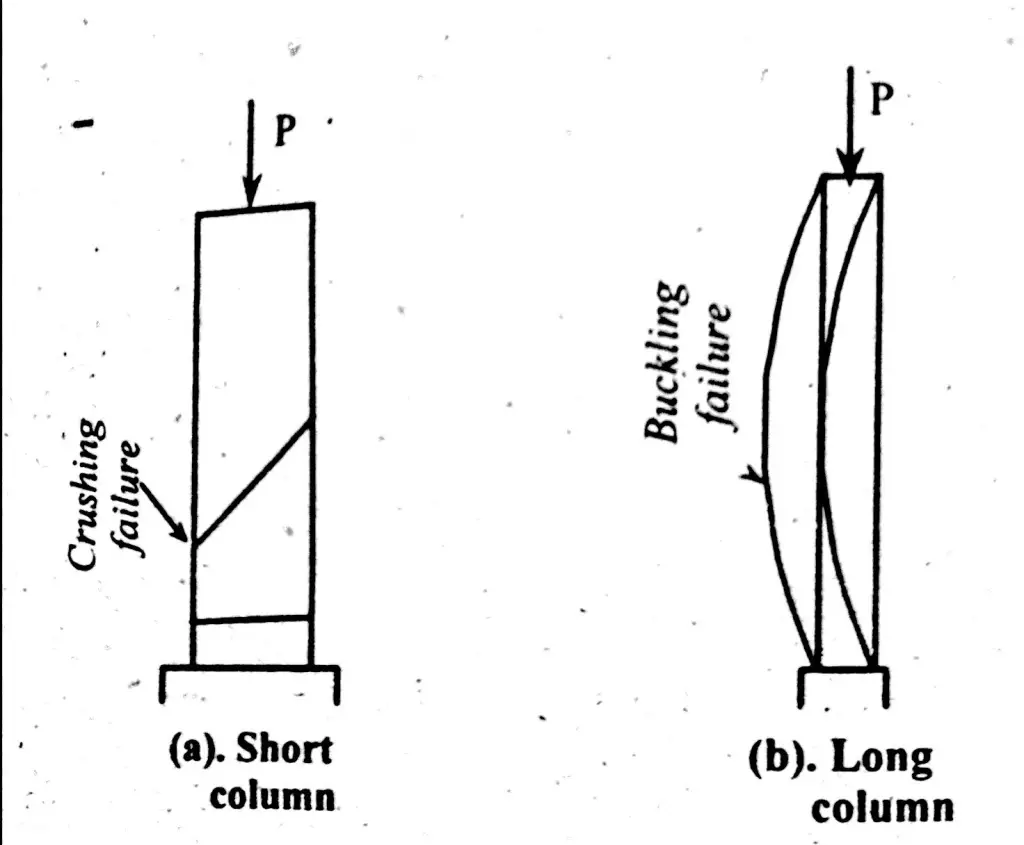
Short Column
If the length of column is 15 times the least dimension of its cross-section, then column will be short column. Slenderness ratio of short column is up to 80. Slenderness ratio is the ratio between effective length of column and radius of gyration.
Long Column
If the length of column is more than 15 times the least dimension of its cross-section, then column will be categorized as long column. Slenderness ratio of long column is more than 80.
Radius of Gyration
If cross-sectional geometry of column is other than simple shapes like circle, square, rectangle etc. Then radius of gyration is required for the calculation of ultimate load that column can carry. Minimum value of radius of gyration is adopted during the design of columns. For getting minimum value, use minimum value of moment of inertia in the formula. Radius of gyration is directly proportional to the moment of inertia.
Radius of Gyration is the minimum radius from the centroid of column cross-section. It is denoted by “K” or “r’’. It is measured in millimeter, centimeter, inches etc..
Radius of Gyration Formula
\(\large K\space\ =\space\ \sqrt\frac{I}{A}\)Mathematically, Radius of gyration can be represented as;
Where,
K = Radius of Gyration
I = Moment of Inertia
A = Cross-sectional Area.
Note: During the design of column, minimum value of radius of gyration is adopted. For that always take least value of moment of inertia in formula.
Column Failure Patterns
Failure pattern of short column is totally different than long column patterns. Short column directly fails at the maximum value of direct stress it can take. In result of this, column material fails and get crushed. Long column buckles on the application of load. Bending stress produces in result of buckling which results in column failure. Short column of same material and same cross section will carry more load as compared to longer column.
Column Loading Patterns
There are two types of column loading patterns. Patterns depend on the location where load is acting. These are;
- Axially Loaded Column
- Eccentric Loaded Column
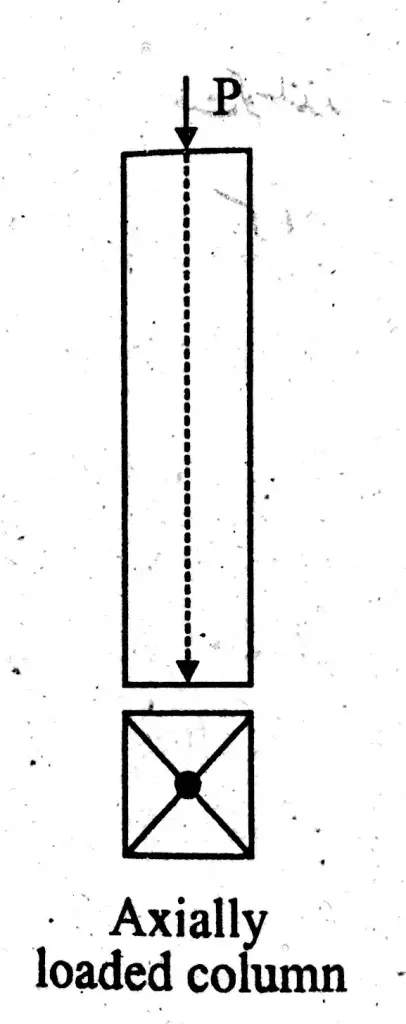
Axially Loaded Column
Axially loaded columns are the one where load acts at the centroid of column cross-section. This is also known as concentric loaded column. Resistance of axial loaded column is more against buckling than eccentric loaded column. As shown in figure below;
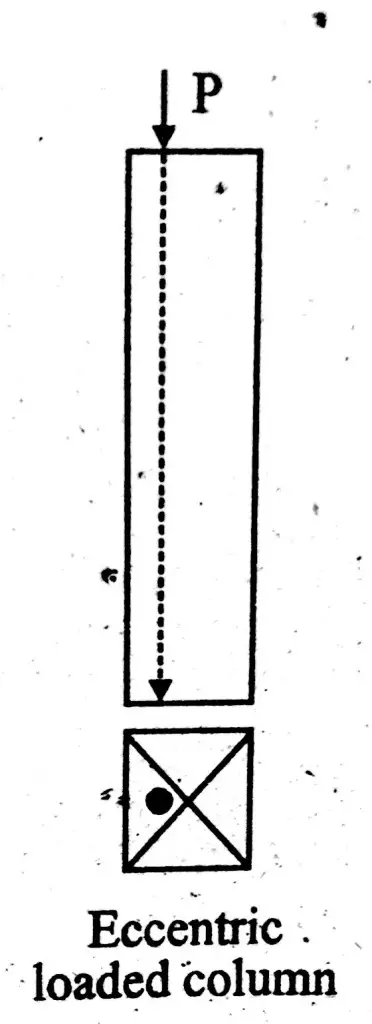
Eccentric Loaded Column
If load acts away from centroid of column cross-section, then such column is known as eccentric loaded column. Resistance of eccentric loaded column against buckling is very less than concentrically loaded column. If both types of loaded columns have same cross-section and material, then axially loaded column will be considered as stronger.
Buckling Load
Buckling load is the minimum load which produces buckling in a column.
Crushing Load
Crushing load is the minimum load which crushes the column material. Value of buckling load will be smaller than crushing load on the same column. During the design of column, neither crushing load nor buckling is load considered. But, little lesser value of load is considered which is coming on column. That value of load is known as safe load. Structures remain safe under safe load.
Factor of Safety
Factor of safety is the ratio between crushing/buckling load and safe load. Generally, factor of safety value ranges between 2 and 5 for structures.
Column End Conditions
How much load a column can bear also depends on column end conditions. Column with a fixed end conditions at both ends will be stronger, then the second column of same size, length and material but having both ends free. Ability to carry load will be different for both columns.
Effective length of a column is calculated after knowing the column end conditions. Effective length changes with the change in column end conditions. Following are the column end conditions.
- Both Ends Hinged
- Both Ends Fixed
- One End Fixed and Other Hinged
- One End Fixed and Other Free
Both Ends Hinged
This is the standard column end condition. Effective length in this condition is equal to the length of column. Effective length of other end conditions can be found with reference to this condition. In this condition, both ends of column are either pinned, pivoted or rounded. As shown in figure below;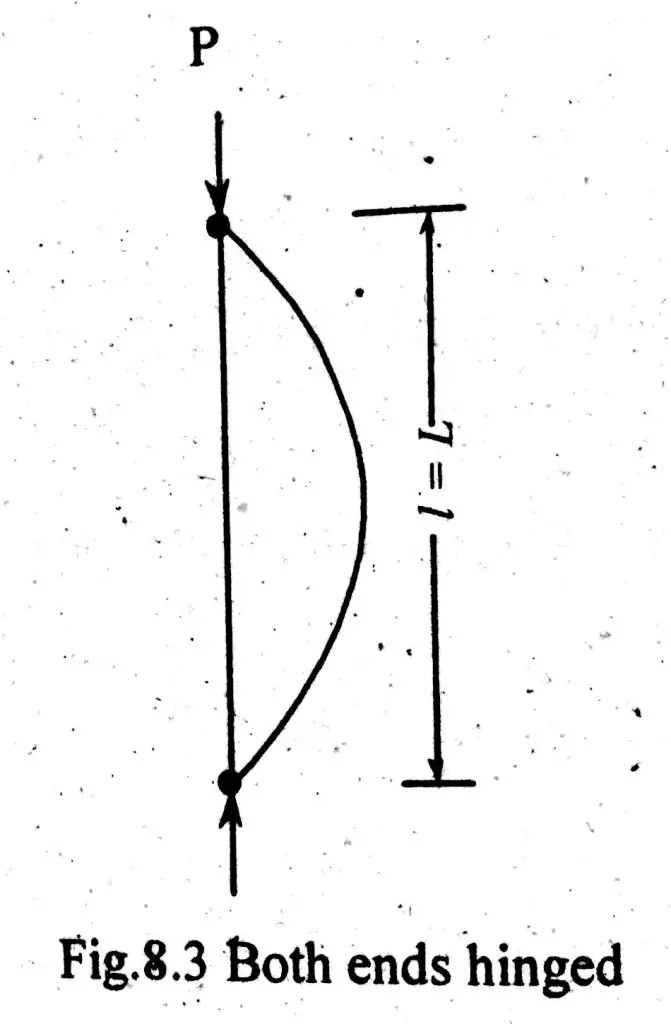
\( \large l\space\ =\space\ L\)
Where,
\( \large l\space\ =\space\ Equivalent\space\ length\)L = Actual Length
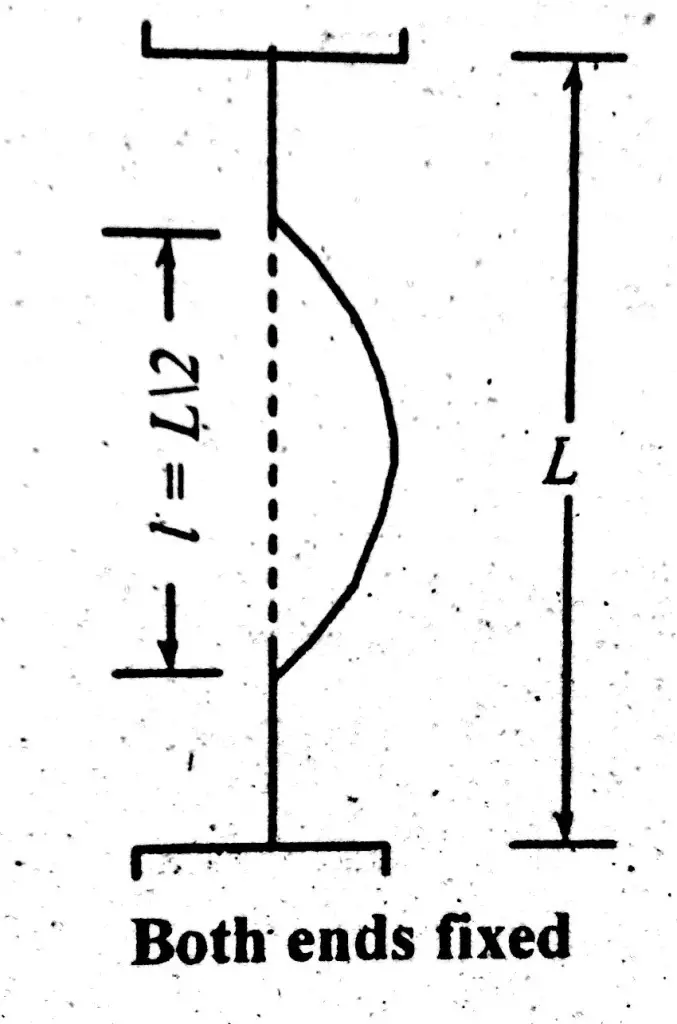
Both Ends Fixed
This is the strongest column end condition. Both ends fixed column carries maximum load and effective length for this condition is considered as half of total column length. Column load bearing capacity increases with the decrease in column equivalent length. As shown in figure below;
\( \large l\space\ =\space\ \frac{L}{2}\)Where,
\(\large l\space\ =\space\ Equivalent\space\ length\)L = Actual Length
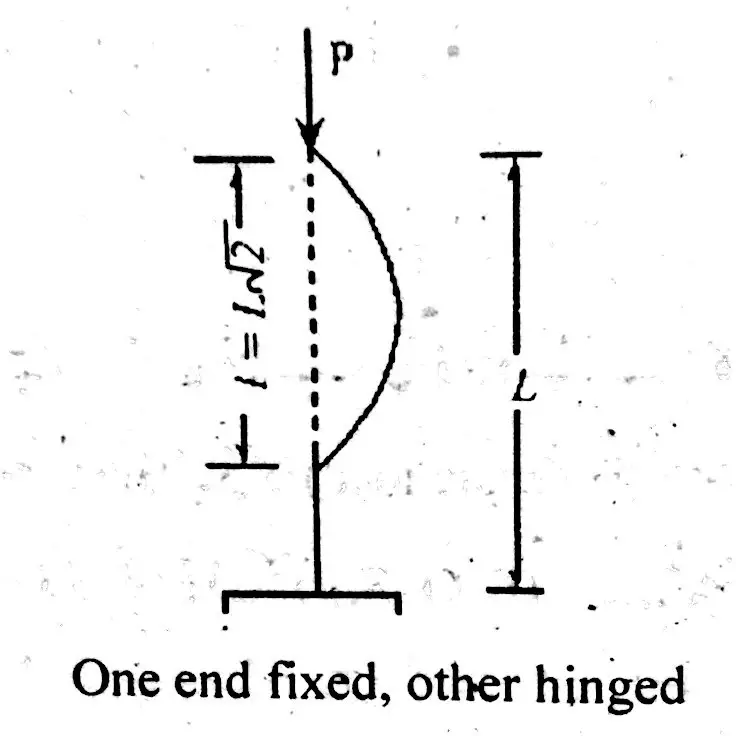
One End Fixed and Other Hinged
In this condition, one end of a column is stronger while the other end is very weak. Equivalent length for this end is as following;
\(\large l\space\ =\space\ \frac{L}{\sqrt{2}}\)One End Fixed and Other Free
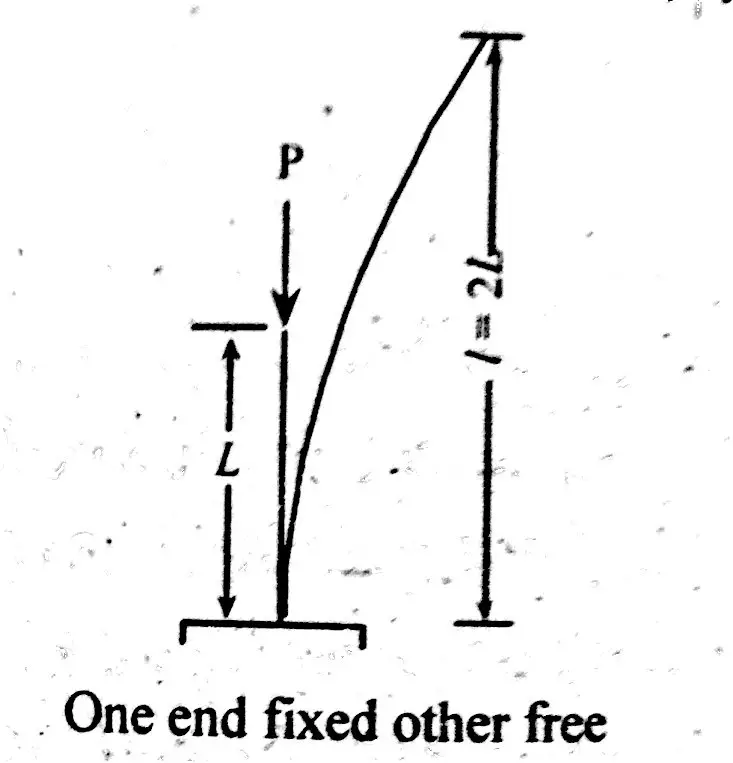
This end condition makes column to bear the smallest load than all other end conditions. Column in such condition is very weak. Equivalent length for one end fixed and other free is as following;
\( \LARGE l\space\ =\space\ 2L\)Column Design Formula’s
There are two formulas used for the design of column. These are;