The algebraic sum of all forces either to left or right side of the exact location of the unknown point treating it as ‘x’ and equate it to zero and solve for ‘x’.
Ra = wx.
The magnitude of Ra is evaluated first and ‘x’ is calculated from the equation shown where ‘Ra’ is the reaction at at origin ‘A’ of the beam.
In order to find point of zero shear or point of maximum bending moment. Let consider an example.
Point of Zero Shear Example
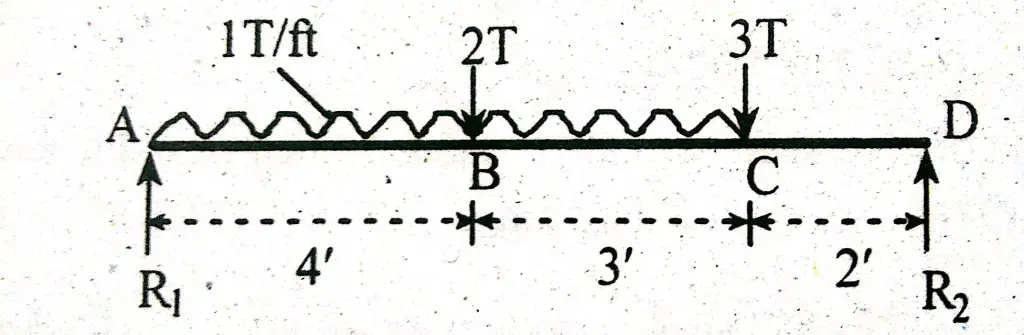
Consider a simply supported beam carrying uniform distributed load and point loads. Find point of zero shear or point of maximum bending moment. As shown below;
Solution
In order to find point of zero shear. First find reactions towards beam because of load acting on it.
For calculation of reaction R1, consider sum of moments at point D is equal to zero. i.e;
\(\sum M_{D}=0\)R1 x 9 = (3×2) + (2×5) + (1×7)(7/2 +2)
R1x9 = 54.5
R1 = 6.056T
Now for calculation of reaction R2
\(\sum M_{A}=0\)R2x9 = (1×7)(7/2) + (3×7) + 2×4
R2x9 = 53.5
R2 = 5.944T
Shear Force
Shear force at A = S.F (A) = 6.056T
Shear force at B(L) = S.F (B) = 6.056 – (1×4) = 2.056T
Shear force at B(R) = S.F (B)= 6.056 – (1×4) – 2 = 0.056T
Shear force at C(L) = S.F(C) = 6.056 – (1×7) – 2 = -2.944T
Shear force at C(R) = S.F(C) = 6.056 – (1×7) – 2 – 3 = -5.944T
Shear Force at D = S.F (D) = – 5.944T
Point of Zero Shear
There are two methods for finding point of zero shear. Both methods are simple.
First Method
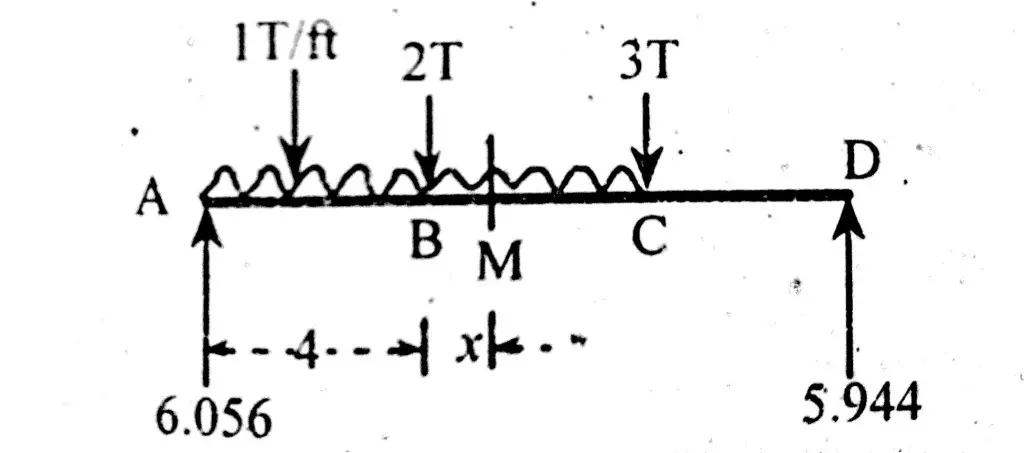
In this method, a random point is assumed. Let say M be the point of zero shear at distance x from point B.
Shear force at point M = 0
As shown in figure below;
6.056 – (1×4) – (1x X) – 2 = 0
X = 0.056ft from point B.
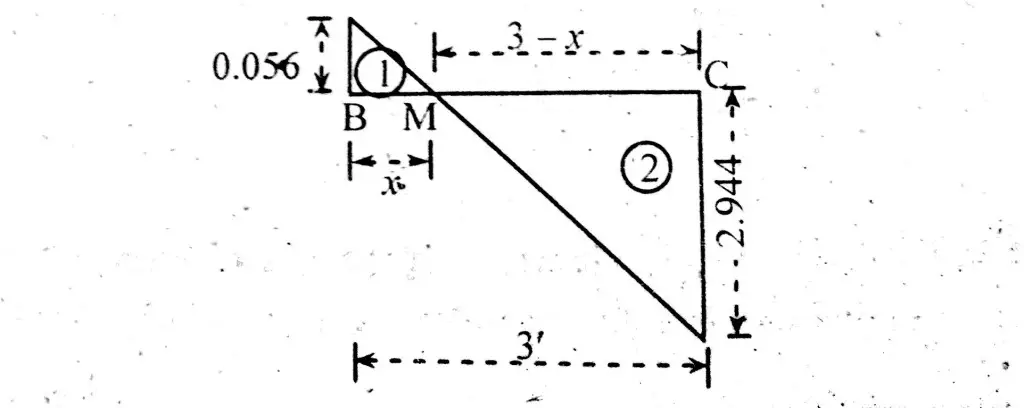
Second Method
In this method, similar triangles from shear force diagram are considered for finding point of zero shear. As shown in figure below;
\(\frac{X}{0.056} = \frac{3 – X}{2.944}\)
2.944X = 0.056(3 – X)
X = 0.056 ft.