How to Find Point of Contraflexure

In an overhanging beam, point of contraflexure is a point where bending moment changes it sign. Example: A point, where bending moment goes from positive to negative or from negative to positive. It can better explained by solving a numerical.

Point of Contraflexure Example

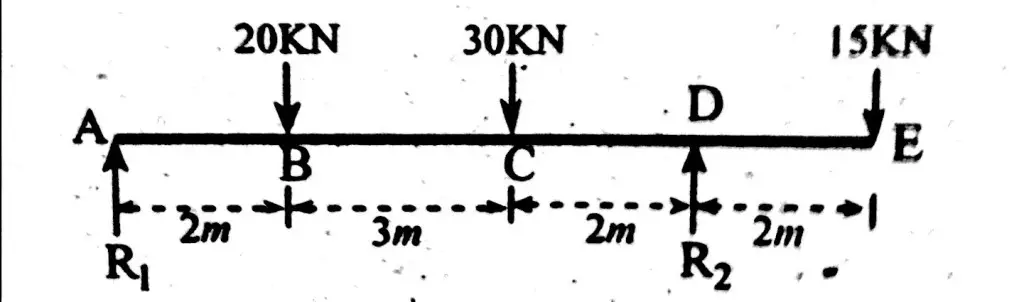
Find point of contraflexure of beam shown below.

Solution

In order to find point of contraflexure, first find the reactions at supports.

Consider,

∑M(at point D) = 0

R1 x 7 + (15 x2) = (30×2) + (20×5)

R1 = 18.571 KN

For Reaction R2, consider;

∑M(at point A) = 0

R2x7 = (20×2) + (30×5) (15×9)

R2 = 46.429 KN

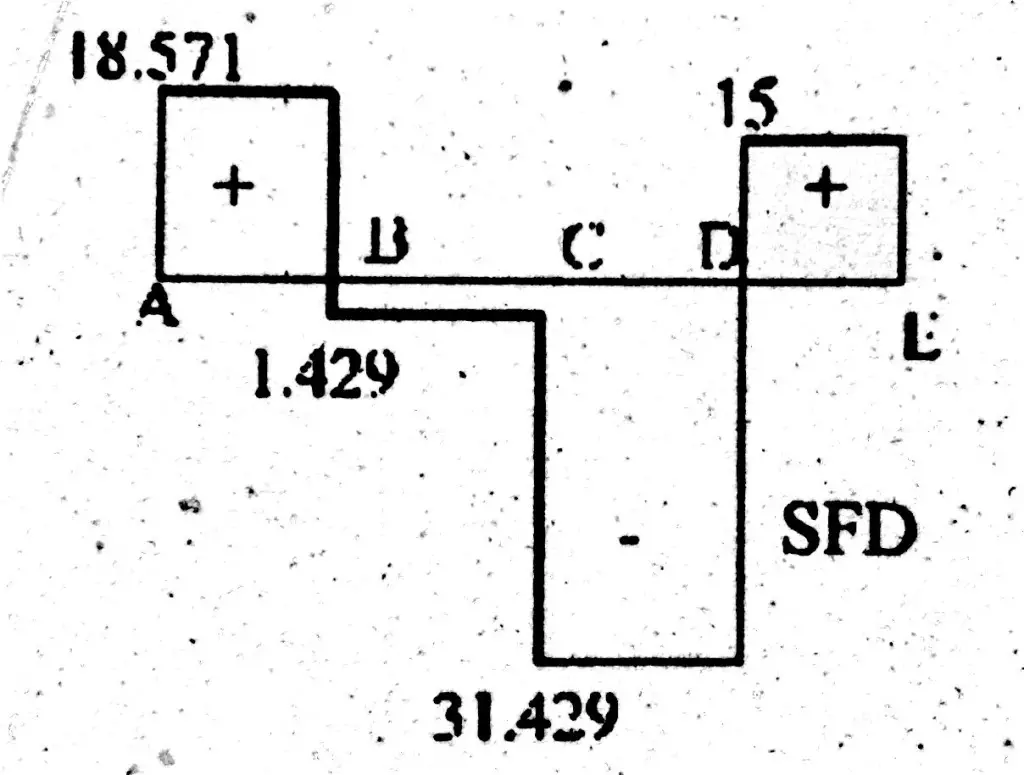
Shear Force Diagram

Next step is to draw a shear force diagram. For shear force diagram, first we have to find shear force at point A, B, C, D and E.

Shear force at point A = S.F_A = 18.571 KN
Shear force at point B(left) = S.F_B(L) = 18.571 KN
Shear force at point B (right) = S.F_B(R) = 18.571 – 20 = 1.429 KN
Shear force at point C (left) = S.F_C(L) = – 1.429 KN
Shear force at point C (right) = S.F_C(R) = 18.571 – 20 – 30 = 31.429 KN
Shear force at point D (left) = S.F_D(L) = -31.429 KN
Shear force at point D (right) = S.F_D(R) = 18.571 – 20 – 30 + 46.429 = 15 KN
Shear force at point E = S.F_E = 15 KN

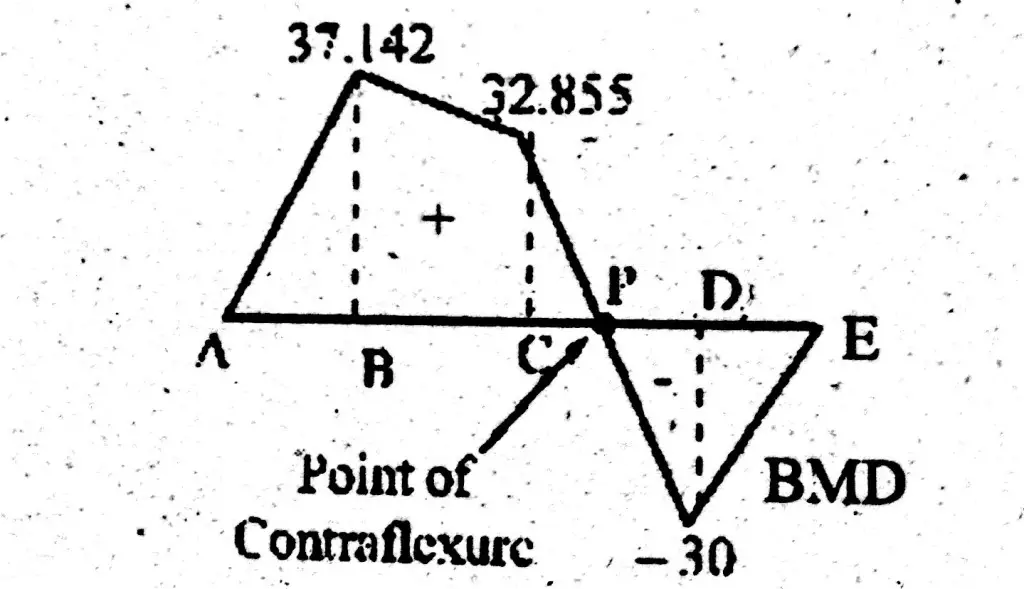
Bending Moment Diagram
Bending Moment at A = 18.571 x 0 = 0

Bending Moment at B = 18.571 x 2 = 37.142 KN.m
Bending Moment at C = (18.571 x 5) – (20 x 3) = 32.855 KN.m
Bending Moment at D = -(15 x 2) = -30KN.m
Bending Moment at E = 0

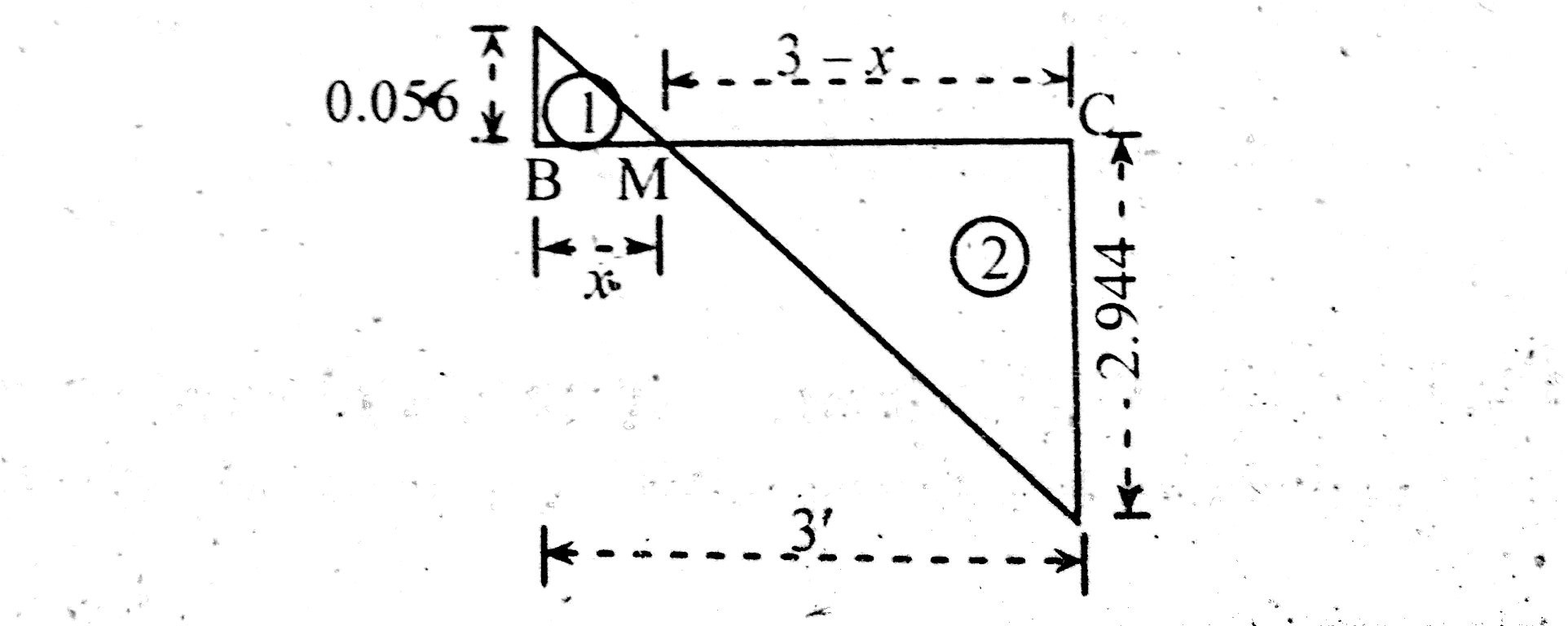
Position of Point of Contraflexure

From bending moment diagram, one can see that bending moment is going from positive to negative after some distance from point C. Let consider this point as P.

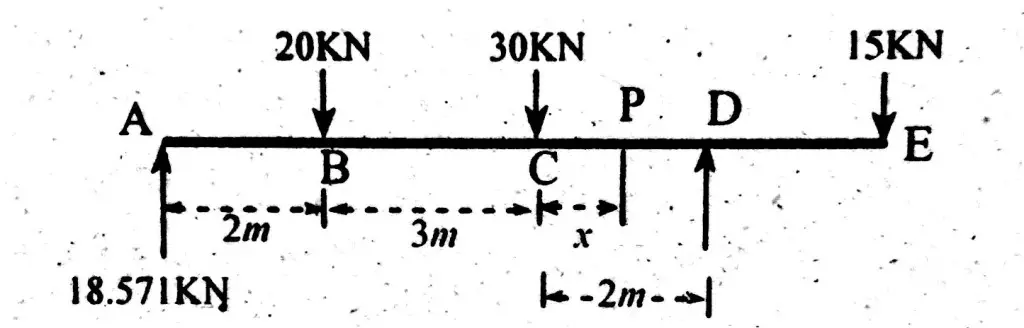
Given “x” distance from point C.
point of contraflexure can be calculated as;
18.571(x + 5) – 20(30*x) = 0
18.571x + 92.855 -20x -60 -30x = 0
31.429x = 32.855
x = 1.045m