This example will help you how to find reactions of simply supported beam when a point load and a uniform distributed load is acting on it.
Example 1
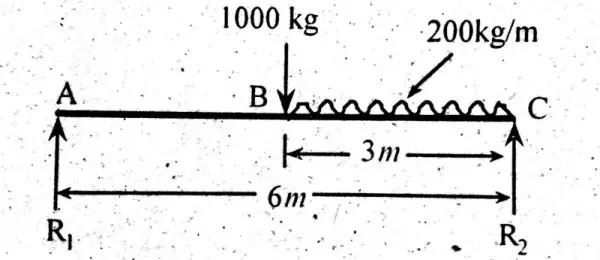
Find reactions of simply supported beam when a point load of 1000 kg and a uniform distributed load of 200 kg/m is acting on it.. As shown in figure below.
Solution
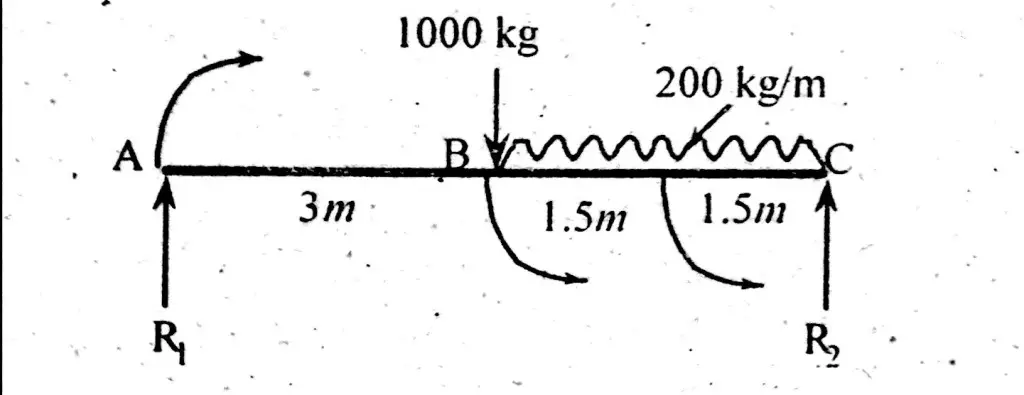
In order to calculate reaction R1, take moment at point C.
\(\sum M_{c}\space = 0\)
Clockwise moments = Anti clock wise moments
R1 x 6 = 1000×3 + (200×3)3/2 = 3600
6R1 = 3000 + 900 = 3900
R1 = 3900/6 = 650 kg.
R1 = 650 kg
for calculating R2 i.e. reaction at point C,
\(\sum F_{V}\space = 0\)R1 + R2 = 600 + 200×4
1300 + R2 = 1400
R2 = 1400 + 1300
R2 = 100 kg
Example II
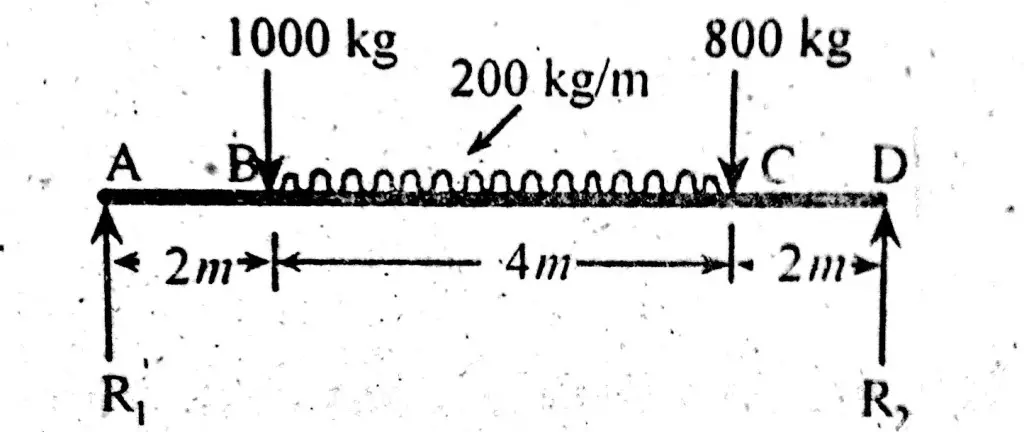
Find reactions of simply supported beam when a point load of 1000 kg & 800 kg along with a uniform distributed load of 200 kg/m is acting on it.. As shown in figure below.
Solution
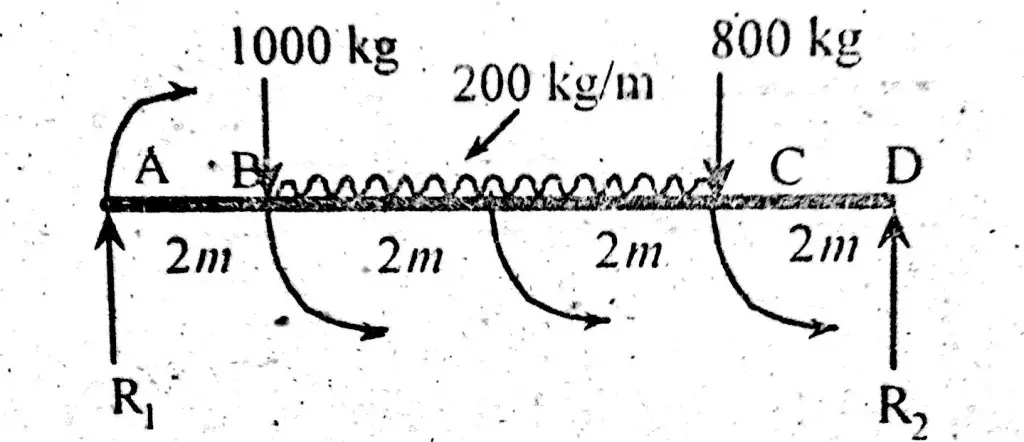
Take moment about point D for finding reaction R1.
\(\sum M_{D}\space = 0\)Clockwise moments = Counter clockwise moments
R1 x 8 = 800 x 2 + (200 x 4) (2 + 2) + 1000 x 6
8R1 = 1600 +3200 + 6000 = 10800
R1 = 1350 Kg.
Now consider all upward forces are equal to downward forces for calculating R2. i.e.
\(\sum F_{V}\space = 0\)R1 + R2 = 1000 + 200 x 4 + 800
1350 + R2 = 2600
R2 = 2600 – 1350
R2 = 1250 Kg.