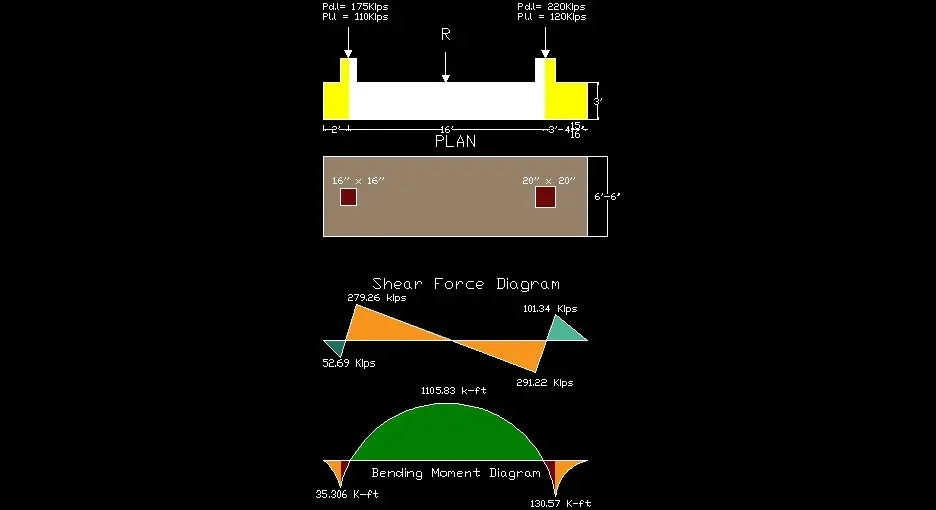
Combined Footing Problem Statement
Design a rectangular combined footing to support two columns shown above. The edge column on the left has a section of 16” x 16” and carries dead & live load of 175 kips & 110 kips respectively. The interior column has a section of 20” x 20” & carries dead & live load of 220 kips & 120 kips respectively. The allowable soil pressure is 5.5 ksf (kips per square foot) and the bottom of footing is 5 ft. below the final grade. Using f’c = 4 ksi & Fy = 60 ksi. Design the footing using ACI Strength design method.
___________________________________________________________________
Combined Footing Problem Solution :
Step 1: Locate the resultant of loads ‘R’.
___________________________________________________________________
Taking moments about center line of left column. The distance of resultant from property line.
\(\bar{x}.R=(200+120) \times 16 \)\(\bar{x}(175+110+220+120) = (340)\times 16 \)
[bar{x} = frac{340*16}{625}]
\(\bar{x}=\frac{340 \times 16}{625} \)The distance of resultant from property line is;
= 2+ 8.704 = 10.704′
In order to have resultant at the middle of footing, the length of footing should be;
L= 10.704 x 2 = 21.41′
Now resultant of applied loads coincides with resultant of upward soil pressure.
Step 2 : Determine the total area of footing
___________________________________________________________________
First find the effective depth of footing
Assume a total depth of footing = 36”
d = Total Depth – Concrete cover – bar dia
d = 36-3 -1.5 = 31.5”
Total applied load = 175 +110 + 220 + 120 = 625 kips.
Net Upward Soil Pressure
\(Net \space Upward \space Pressure=5500 \space – \frac{36}{12} \times 150 + \frac{24}{12} \times 120 \)
Net Upward Soil Pressure = 4810 psf = 4.810 ksf
Required Area of footing = 628/4.810 = 130 ft²
Width of footing = 130 / Length of footing = 130 / 21.41
Width of footing = 6.07′ take 6.5′
We have chosen a footing with the length of 21.41′ and width of 6.5′, giving an area of 139.165 sq.ft .
Step 3 : Determine Factored Upward Pressure
__________________________________________________________________
Pu (Left Column) = 1.2 x 175 + 1.6 x 110 = 210 + 176
Pu (Left Column) =386 Kips
Pu (Right Column) = 102 x 220 + 1.6 x 120 = 264 +176
Pu ( Right Column) = 456 Kips
Net Factored soil pressure = qu = (386 +456)/139.16 = 6.05 ksf
Step 4: Draw Factored Shear Force Diagram & Bending Moment Diagram
__________________________________________________________________
Considering the footing as a beam of 21.4′ span supported on two columns and subjected to a uniform upward pressure of
6.05 x 6.5 = 39.325 k/ft
Va + Vb = 39.325 x 21.41 = 841.95 Kips
∑Ma = 0 Vb x 16 = 39.325 x 21.41 x[(21.41/2) – 2)]
Vb = 458.07 Kips (look at shear force diagram i.e. already plotted)
Va = 841.95 – 458.07 = 383.87 Kips ( As shown in the below diagram)
Vu (at outer face of left column) = 39.325 x ( 2 – 0.66)
Vu = – 52.69 Kips
Vu(at inner face of left column) = 39.325x(2+0.66) – 383.87
Vu = +279.26 Kips
Vu(at outer face of right column) = 39.325x( 3.41- 0.833)
Vu(at outer face of right column) = + 101.34 kips
Vu(at inner face of right column) = 39.325 x (3.41 + 0.833) – 458.07
Vu(at inner face of right column) = – 291.22 Kips
So, Shear force diagram can be plotted. Now locate a point of zero shear. Compare similar triangles or write a generalized shear force expression for mid span and set it to zero.
\(\frac{279.26}{x}=\frac{291.22}{14.51-x}\)
X = 7.10′
Step 5: Draw Factored Bending Moment Diagram
___________________________________________________________________
Moment at the outer face of left column;
M = 39.325x[(2-0.66)/2]^2 = – 35.306 k-ft
Moment at the outer face of right column;
M = 39.325x[(3.41 – 0.833)/2]² = -130.57 k-ft
Maximum Positive Moment;
M = -39.325 x [(2+7.1 + 0.66)/2]² + 383.87 x(7.1 + 0.66)
M = – 1873 + 2978.83
M = + 1105.83 K-ft.
Now we will check the depth of footing for one way shear and two way shear.
Step 6: Check Depth of Footing for One Way Shear
__________________________________________________________________
From shear force diagram, maximum shear occurs at the critical sections, located at a distance ”d” from the interior face of right column, as shown in the loading diagram above.
Vu (at critical Section) = 291.22 – 39.325 x (31.5/2)
Vu(at critical section) = 188 Kips
d =Vu/Φ2b√f’c = 188×1000/0.75x2x6.5×12*√4000
d = 25.4”< 31.5 ”
Hence, depth of footing is adequate against one way shear.
Step 7: Check for Two Way Shear
___________________________________________________________________
Two way shear or punching shear can be determined from critical perimeter b0.
For Interior Column;
b0 = 4x(c + d) = 4 x (20 + 31.5)
b0 = 17.17 ft. C + d = (20 + 31.5) / 12 = 4.29 ft.
Shear at d/2 from all sides of this column is;
Vu = Pu – qu (C + d)^2
Vu = 456 – 6.05(4.29)^2
Vu = 344.65 Kips
d =Vu/Φ(4√f’c)b0 = (344 x 1000)/0.75(4x√4000)x 17.17x 12
d = 8.81” <31.5” →ok
The Depth of footing is adequate with respect to two way shear or punching shear.
Step 8: Check The Depth of Moment & Calculate Required Moment:
____________________________________________________________________
From Bending moment diagram:
Maximum bending moment = 1105.83 k-ft
The depth would be adequate
Mu/Φbd² = (1105.83 x 1000)/ (0.9 x 6.5 x 12 x 31.5²) = 190.51 psi.
ρ = (0.85xf’c)/fy[1- √1 – (2Mu)/Φbd²/0.85f’c) ]
ρ = (0.85 x 4)/60 [1 – √1 – (2 x 190.5)/ 0.85 x 4000 ]
ρ = 0.00322 As = ρbd = 0.00322 x 6.5 x 12 x 31.5
As = 7.91 in²
ρmin = 0.0018
As min = ρmin x bd = 0.0018 x 6.5 x 12 x 36
As min = 5.05 in.
Choose 8 #9- bars (As = 7.91 in²)
Bar Spacing:
____________
S = (6.5 x12 – 2 x3)/ 8 S = 10.28”
These bars are extended between the columns at top of footing with concrete cover of 3” as place minimum reinforcement corresponding to temperature and shrinkage reinforcement, corresponding to minimum area of 5.5 in². Use (7 #8 bars) they provide an area (As = 5 in²).
Place this reinforcement at the bottom of projecting ends of footings beyond columns to take care of positive moments (see the bending moment diagram). Extend these bars by a development length beyond sides of the columns.
Development Length (ld) for top bars = 1.3 ld = 1.3 x 54 ld = 70″
Reinforcement in the short direction.
Now calculate the bending moment in shorter direction. The reinforcement under each column is to placed within a maximum band width equal to column width plus twice the effective depth of footing.
Use full width of 6.5 ft as band width for concentrating reinforcement under;
Left Column
_____________
Net Upward Pressure = Pu1/ width of footing = 386/6.5
Net Upward Pressure = 59.38 k/ft
Distance from free end to the face of left column. 2 – 8/12 = 1.33′
Mu at the face of left column. = 59.38 x (1.33)²/2 = 52.51 K-ft.
Assume jd = 0.9d d = 31.5″
Mu = ΦTjd = ΦAsfy jd As = Mu/ Φfyjd = (52.51 x 12000)/(0.9 x 60,000 x 0.9 x 31.5”)
As = 0.411 in² → Provide (As)min = 7 #8 bars (5.05 in²)
Right Column
_______________
Net Upward Pressure under Right column = Pu2/ Width of footing = 456 / 6.5
Net Upward Pressure = 70.15 K/ft
Mu at face of right column = 70.15 x (2.57)²/2 = 231.66 k-ft.
As = (231.66 x 12000)/(0.9 x 60,000 x 28.35)
As = 1.81 in² → Provide minimum As = 7 # 8 bars (5.5 in²)