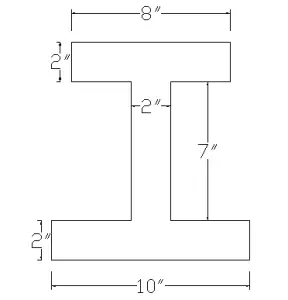
Centroid of I-section can be found easily with respect to reference x-axis because of section symmetry around y-axis. As shown in the example below;
Example
Find the centroid of I-section given below.
Solution
Step: 1
First divide the whole section into parts i.e., rectangles and find the area of every single rectangle in a section.
There are three rectangles in I-section.
Area of 1st rectangle = 2″x 8″ = 16 sq. inch
Area of 2nd rectangle = 2″x 7″ = 14 sq. inch
Area of 3rd rectangle = 2″x 10″ = 20 sq. inch
Summation of Areas = 16 + 14 + 20 = 50 sq. inch
Step: II
Find the centroid of each portion with respect to y-axis i.e., with reference to x-axis
Centroid of 1st rectangle with respect to reference x-axis = 2/2 + 9 = 10 in.
Centroid of 2nd rectangle with respect to reference x-axis = 7/2 + 2 = 5.5 in.
Centroid of 3rd rectangle with respect to reference x-axis = 2/2 = 1 in.
Step: III
Find the moment of areas = (Area) x (Centroidal distance Y from x-axis)
Moment of area of 1st rectangle = 20 x 1 = 20
Moment of area of 2nd rectangle = 14 x 5.5 = 77
Moment of area of 1st rectangle = 16 x 10 = 160
Summation of moment of areas = 20 + 77 + 160 = 257
Step : IV
Put values in the centroid formula;
\(\bar{Y}=\frac{Sum\space\ of\space\ moments}{sum\space\ of\space\ Area}\)